Question

【题目】在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．

（1）用树状图或列表法列举点M所有可能的坐标；

（2）求点M（x，y）在函数y=﹣的图象上的概率．

Answer 1

【答案】（1）答案见解析（2）

【解析】

试题分析：（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；

（2）由点M（x，y）在函数y=﹣的图象上的有（1，﹣2），（2，﹣1），直接利用概率公式求解即可求得答案．

解：（1）画树状图得：

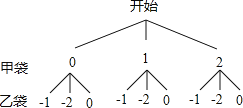
则共有9种等可能的结果：（0，﹣1），（0，﹣2），（0，0），（1，﹣1），（1，﹣2），（1，0），（2，﹣1），（2，﹣2），（2，0）；

（2）∵点M（x，y）在函数y=﹣的图象上的有（1，﹣2），（2，﹣1），

∴点M（x，y）在函数y=﹣的图象上的概率为：．