题目内容
把三张大小相同的正方形卡片A,B,C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图1摆放时,阴影部分的面积为S1;若按图2摆放时,阴影部分的面积为S2,则S1 S2(填“>”、“<”或“=”).


=
 根据正方形的性质,可以把两块阴影部分合并后计算面积,然后,比较S1和S2的大小.
根据正方形的性质,可以把两块阴影部分合并后计算面积,然后,比较S1和S2的大小.解:设底面的正方形的边长为a,正方形卡片A,B,C的边长为b,
由图1,得S1=(a-b)(a-b)=(a-b)2,
由图2,得S2=(a-b)(a-b)=(a-b)2,
∴S1=S2.
故填:=.
本题主要考查了正方形四条边相等的性质,分别得出S1和S2的面积是解题关键.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
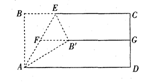
 .
.
 ;
; ,求
,求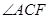 的度数.
的度数.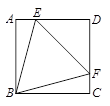
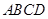 中,
中,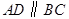 ,
,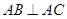 ,
,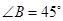 ,
,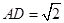 ,
,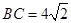 ,求
,求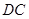 的长.
的长.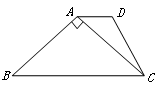
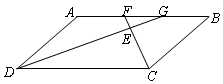
 =BC.∴∠NMC=180°—∠AMN—∠
=BC.∴∠NMC=180°—∠AMN—∠ AMB=180°—∠B—∠AMB=∠MAB
AMB=180°—∠B—∠AMB=∠MAB
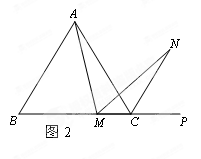
 边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)