题目内容
如图，正方形ABCD中，AB=4，点E，F分别在AD，DC上，且△BEF为等边三角形，则△EDF与△BFC的面积比为（ ）．
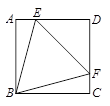
| A．2:1 | B．3:1 | C．3:2 | D．5:3 |
A
解：因为三角形BEF是等边三角形
所以BE=BF
EBF=60
因为ABCD是正方形
所以ABC=BAE=BCF=90
AB=BC=4
所以Rt
BAE
RtBCF（HL）
所以ABE=CBF
因为ABC=ABE+CBF+EBF=60
所以CBF=15所以BF=
=4(
）
CF=8-4
所以BEF的面积=
=4（8-4）
三角形BFC的面积=
=2（8-4）
所以BEF的面积与BFC的面积比是：2:1
所以BE=BF
EBF=60因为ABCD是正方形
所以
ABC=BAE=BCF=90AB=BC=4
所以Rt
BAERtBCF（HL）所以
ABE=CBF因为
ABC=ABE+CBF+EBF=60所以
CBF=15所以BF==4(）CF=8-4
所以
BEF的面积==4（8-4）三角形BFC的面积=
=2（8-4）所以
BEF的面积与BFC的面积比是：2:1
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
，求证四边形DEBF是菱形．
的面积为12，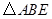
是等边三角形，点
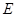在正方形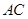
上有一点
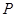，使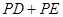
的和最小，则这个最小值为________
