题目内容
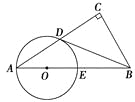
【题目】如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E,
(1)求证:CF=CG;
(2)连接DE,若BE=4CE,CD=2求DE的长.

【答案】(1)证明见解析;(2)DE=![]()
【解析】分析:(1)连接AC,首先可通过DG∥AB,AB=BC证得AC为∠DCE的角平分线,从而得到△ADC≌△AEC,可知CD=CE;再由∠FDC=∠GEC=90°,∠FCD=∠GCE,可判定△FDC≌△GEC,即可得CF=CG.(2)由已知条件,可求得AE、AC的长,法一:可利用C、A分别是DE垂直平分线上的点,并通过解直角三角形AEC的面积求得EH的长,从而得到ED的长.法二:通过证明△ADE∽△BAC可得![]() ,从而求得DE的长.
,从而求得DE的长.
本题解析:
(1)证明:连接AC

∵DC∥AB,AB=BC, ∴∠1=∠CAB, ∠CAB=∠2,
∴∠1=∠2,∠ADC=∠AEC=90°,AC=AC,
∴△ADC≌△AEC,∴CD=CE
∵∠FDC=∠GEC=90°, ∠3=∠4, ∴△FDC≌△GEC,
∴CF=CG,
(2)解:由(1)知,CE=CD=2,∴BE=4CE=8,∴AB=BC=CE+BE=10,
∴在RT△ABE中,AE=![]() ,
,
∴在RT△ACE中,AC=![]() ,
,
法一:由(1)知,△ADC≌△AEC,∴CD=CE,AD=AE,
∴C、A分别是DE垂直平分线上的点,
∴DE⊥AC,DE=2EH,
在RT△AEC中, ![]() ,
,
∴![]() ,
,
∴DE=2EH=2×![]() .
.
法二:在RT△AEC中,∠2+∠6=90°,
在RT△AEH中,∠5+∠6=90°,∴∠2=∠5,
∵AD=AE,AB=BC, ∴∠5=∠7,∠CAB=∠2
∴∠7=∠CAB,∴△ADE∽△BAC,
∴![]() , 即
, 即![]() ,
,
∴DE=![]() .
.

 阅读快车系列答案
阅读快车系列答案