题目内容
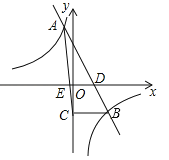
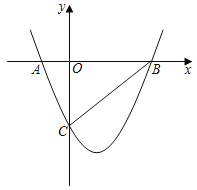
【题目】在平面直角坐标系xOy中,抛物线y1=2x2+![]() 的顶点为M,直线y2=x,点P(n,0)为x轴上的一个动点,过点P作x轴的垂线分别交抛物线y1=2x2+
的顶点为M,直线y2=x,点P(n,0)为x轴上的一个动点,过点P作x轴的垂线分别交抛物线y1=2x2+![]() 和直线y2=x于点A、点B
和直线y2=x于点A、点B
(1)直接写出A、B两点的坐标(用含n的代数式表示)
(2)设线段AB的长为d,求d关于n的函数关系式及d的最小值,并直接写出此时线段OB与线段PM的位置关系和数量关系;
(3)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+![]() ,求a,b,c的值.
,求a,b,c的值.
【答案】(1)A(n,2n2+![]() ),B(n,n);(2)d=2(n﹣
),B(n,n);(2)d=2(n﹣![]() )2+
)2+![]() ,d最小值
,d最小值![]() ,此时线段OB与线段PM的位置关系和数量关系是OB⊥PM且OB=PM;(3)a=1,b=1,c=0.
,此时线段OB与线段PM的位置关系和数量关系是OB⊥PM且OB=PM;(3)a=1,b=1,c=0.
【解析】
(1)由题意不难看出:点P、A、B三点的横坐标相同,将点P横坐标代入函数y1、y2的解析式中即可确定A、B两点的坐标.
(2)首先根据题意画出图形,可看出抛物线y1的图象始终在直线y2的上方,那么线段AB的长可由点A、B的纵坐标差求得,据此求出关于d、n的函数解析式,根据函数的性质先确定出符合题意的n、d值,即可确定点B、P的坐标,点M的坐标易得,根据这四点坐标即可确定线段OB、PM的位置和数量关系.
(3)首先将函数解析式代入不等式中,再根据利用函数图象解不等式的方法来求出待定系数的取值范围,最后根据a、b、c都是整数确定它们的值.
(1)当![]() 时,
时,![]() ;
;
∴![]() .
.
(2)![]() .
.
∴![]() .
.
∴当![]() 时,d取得最小值
时,d取得最小值![]() .
.
此时,B(![]() ,
,![]() ),而M(0,
),而M(0,![]() )、P(
)、P(![]() ,0),
,0),
∴四边形OMBP是正方形,
∴当d取最小值时,线段OB与线段PM的位置关系和数量关系是OB⊥PM且OB=PM.(如图)
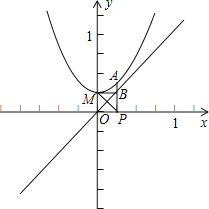
(3)∵对一切实数![]() 恒有
恒有![]() ,
,
∴对一切实数![]() ,
,![]() 都成立
都成立![]() ①
①
当![]() 时,①式化为
时,①式化为![]() .
.
∴整数c的值为0.
此时,对一切实数![]() ,
,![]() 都成立
都成立![]()
即 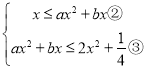 对一切实数
对一切实数![]() 均成立.
均成立.
由②得 ![]()
![]() 对一切实数
对一切实数![]() 均成立.
均成立.
∴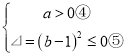 .
.
由⑤得整数![]() 的值为1.
的值为1.
此时由③式得,![]() 对一切实数
对一切实数![]() 均成立
均成立![]()
即![]() 对一切实数x均成立
对一切实数x均成立![]()
当![]() 时,此不等式化为
时,此不等式化为![]() ,不满足对一切实数
,不满足对一切实数![]() 均成立.
均成立.
当![]() 时,∵
时,∵![]() 对一切实数x均成立,(a≠0)
对一切实数x均成立,(a≠0)
∴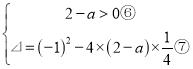
∴由④,⑥,⑦得![]() .
.
∴整数![]() 的值为1.
的值为1.
∴整数![]() 的值分别为
的值分别为![]() .
.