题目内容
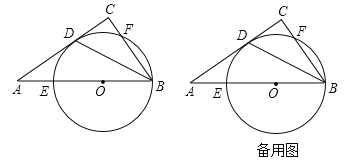
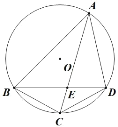
【题目】已知：如图，四边形 ABCD 内接于⊙ O ，AC 和 BD 相交于E ， BC = CD = 4 ， AE = 6 ，且 BE 和 DE 的长是正整数，求 BD 的 长．
【答案】7
【解析】
根据已知条件，易证△ABC∽△BEC，所以BC2=CEAC，即可求得EC=2，再证△BCE∽△ADE，可得BEDE的值，又线段BE、ED为正整数，且在△BCD中，BC+CD>BE+DE，所以可得BE、DE的长，即可得BD的长．
解：∵BC=CD，
∴∠BAC=∠DAC，
∵∠DBC=∠DAC，
∴∠BAC=∠DBC，
又∵∠BCE=∠ACB，
∴△ABC∽△BEC，
∴
，
∴BC2=CEAC，
∵BC=CD=4，AE=6，
∴EC=2，
∵∠DBC=∠DAC，∠CEB=∠DEA，
∴△BCE∽△ADE，
∴
，
∴BEDE=AEEC，
即BEDE=12，
又线段BE、ED为正整数，
且在△BCD中，BC+CD>BE+DE，
所以可得BE=3、DE=4或BE=4、DE=3，
所以BD=BE+DE=7．
练习册系列答案
相关题目
