题目内容
【题目】如图,在平面直角坐标系xOy中,抛物线C1:y=a(x- ![]() )2+h分别与x轴、y轴交于点A(1,0)和点B(0,-2),将线段AB绕点A逆时针旋转90°至AP.
)2+h分别与x轴、y轴交于点A(1,0)和点B(0,-2),将线段AB绕点A逆时针旋转90°至AP.
(1)求点P的坐标及抛物线C1的解析式;
(2)将抛物线C1先向左平移2个单位,再向上平移1个单位得到抛物线C2 , 请你判断点P是否在抛物线C2上,并说明理由.
【答案】
(1)解:∵A(1,0)和点B(0,-2),
∴OA=1,OB=2,过P作PM⊥x轴于M,
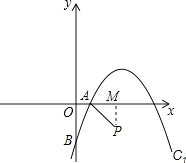
由题意得:AB=AP,∠BAP=90°,
∴∠OAB+∠PAM=∠ABO+∠OAB=90°,
∴∠ABO=∠PAM.
在△ABO于△APM中,
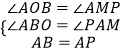 ,
,
∴△ABO≌△APM,
∴AM=OB,PM=OA,
∴P(3,-1),
∵A(1,0)和点B(0,-2)在抛物线C1:y=a(x- ![]() )2+h上,
)2+h上,
∴
解得: 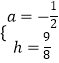 ,
,
∴抛物线的解析式 ![]()
(2)解:∵将抛物线C1先向左平移2个单位,再向上平移1个单位得到抛物线C2,
∴y=- ![]() (x-
(x- ![]() +2)2+
+2)2+ ![]() +1,
+1,
∴抛物线C2的解析式为:y=- ![]() (x-
(x- ![]() )2+
)2+ ![]() ,
,
当x=3时,y=- ![]() (3-
(3- ![]() )+
)+ ![]() =-1,
=-1,
∴点P在抛物线C2上.
【解析】(1)由点A和点B的坐标,用待定系数法求出抛物线的解析式,由已知条件得到△ABO≌△APM,得到对应边相等,求出点P的坐标;(2)根据平移的性质,由顶点式得到抛物线C2的解析式,把P点的坐标代入,得到点P在抛物线C2上.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】中考前的模拟考试对于学生来说具有重大的指导意义,现抽取m名学生的数学一模成绩进行整理分组,形成如下表格(x代表成绩,规定x>140为优秀),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
A组 | 140<x≤150 |
B组 | 130<x≤140 |
C组 | 120<x≤130 |
D组 | 110<x≤120 |
E组 | 100<x≤110 |
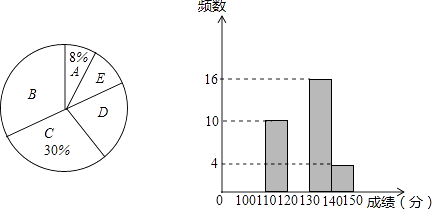
(1)m的值为;扇形统计图中D组对应的圆心角是°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).





