题目内容
【题目】如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE= . 
【答案】12或5
【解析】解:作AF⊥CE于F,DM⊥AF于M,如图所示:
则四边形DEFM是矩形,AF=17,∠AMD=90°,
∴∠EDM=90°,
∵四边形ABCD是正方形,
∴AD=CD=13,∠ADC=∠EDM=90°,
∴∠ADM=∠CDE,
在△ADM和△CDE中, 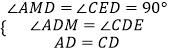 ,
,
∴△ADM≌△CDE(AAS),
∴DM=DE,AM=CE,
∴四边形DEFM是正方形,
∴DM=FM,
设AM=CE=x,则DM=FM=17﹣x,
在Rt△ADM中,由勾股定理得:x2+(17﹣x)2=132,
解得:x=12或x=5,
∴CE=12,或CE=5;
故答案为:12或5.
作AF⊥CE于F,DM⊥AF于M,由AAS证明△ADM≌△CDE,得出DM=DE,AM=CE,证出四边形DEFM是正方形,得出DM=FM,设AM=CE=x,则DM=FM=17﹣x,在Rt△ADM中,由勾股定理得出方程,解方程即可.

练习册系列答案
相关题目