题目内容
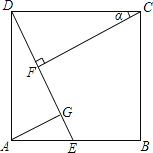
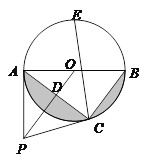
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
【答案】(1)见解析; (2)![]() ;(3) CE的长为
;(3) CE的长为![]() cm
cm
【解析】分析:(1)连接OC,证明△PAO≌△PCO,得到∠PCO=∠PAO=90°,证明结论;(2)证明△ADP∽△ODA,得到成比例线段求出BC的长,根据S阴=SO-S△ABC求出答案;(3)连接AE、BE,作BM⊥CE于M,分别求出CM和EM的长,求和得到答案.
详解:证明: ⑴如图,连接OC,∵PA切⊙O于A.
∴∠PAO=90.
∵OP∥BC,∴∠AOP=∠OBC,∠COP=∠OCB.∵OC=OB,∴∠OBC=∠OCB,
∴∠AOP=∠COP.
又∵OA=OC,OP=OP, ∴△PAO≌△PCO (SAS).∴∠PAO=∠PCO=90 ,
又∵OC是⊙O的半径,
∴PC是⊙O的切线.

⑵解法不唯一. 解:由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90 ,∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD =∠AOD,
∴△ADO∽△PDA.
∴![]() ,∴
,∴![]() ,∵AC=8, PD=
,∵AC=8, PD=![]() ,
,
∴AD=![]() AC=4,OD=3,AO=5,
AC=4,OD=3,AO=5,
由题意知OD为△ABC的中位线,∴BC=2OD=6,AB=10.
∴S阴=S半⊙O-S△ACB=![]() .
.
答:阴影部分的面积为![]() .
.
(3)如图,连接AE,BE,过点B作BM⊥CE于点M.
∴∠CMB=∠EMB=∠AEB=90,又∵点E是![]() 的中点,
的中点,
∴∠ECB=∠CBM=∠ABE=45,CM=MB =![]() ,BE=ABcos450 =
,BE=ABcos450 =![]() ,
,
∴ EM=![]() ,/span>∴CE=CM+EM=
,/span>∴CE=CM+EM=![]()
![]() .
.
答:CE的长为![]() cm.
cm.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?