题目内容
【题目】已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.
【答案】∠COD=5°或∠COD=125°.
【解析】
分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况进行解答,当射线OC在∠AOB的内部时,设∠AOC=2x,则∠COB=3x,计算出x的值,进而计算出∠AOC、∠AOD的度数,从而得出结论.当射线OC在∠AOB的外部时,设∠AOC=2x,则∠COB=3x,则∠AOB=x,得x的值,进而计算出∠AOC与∠AOD的度数,然后得出结论.
分两种情况讨论:
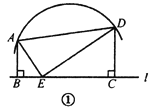
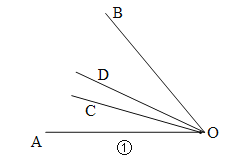
(1)射线OC在∠AOB的内部,如图①;
设∠AOC=2x,则∠COB=3x,则2x+3x=50°,∴x=10°,∠AOC=2x=20°,∠AOD![]() 50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
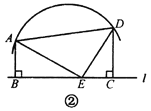
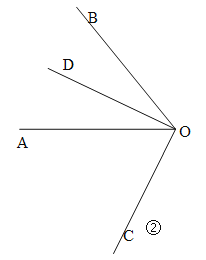
(2)射线OC在∠AOB的外部,如图②.
设∠AOC=2x,则∠COB=3x,则∠AOB=3x﹣2x=x=50°,∴∠AOC=2x=100°
∠AOD=25°,∴∠COD=∠AOC+∠AOD=100°+25°=125°.
综上所述:∠COD=5°或∠COD=125°.

练习册系列答案
相关题目