��Ŀ����
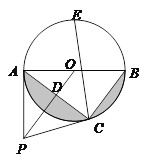
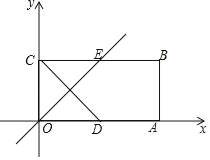
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���B������Ϊ��4��2����D��OA���е㣬OE��CD��BC�ڵ�E����P�ӵ�O��������ÿ��2����λ���ȵ��ٶ�������OE�˶���
��1����ֱ��OE�Ľ���ʽ��
��2������C��P��D��BΪ������ı��ε����ΪS����P���˶�ʱ��Ϊt����λ���룩����S����t�ĺ�������ʽ����д���Ա���t��ȡֵ��Χ��
��3�����NΪ���ε����ģ����ڵ�P�˶������У��Ƿ���ڵ�P��ʹ��P��C��NΪ�������������ֱ�������Σ������ڣ���ֱ��д��t��ֵ����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=x����2��S=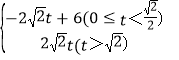 ����3�����ڣ� t=
����3�����ڣ� t=![]() ʱ��P��
ʱ��P��![]() ��
��![]() ����t=
����t=![]() ʱ��P��2��2����t=
ʱ��P��2��2����t=![]() ʱ��P��3��3����
ʱ��P��3��3����
������������: ��1���������COE=45�㣬�������CE=OC=2�����ɵó����ۣ�
��2���ֵ�P��OM����ME��OE���ӳ����ϣ���������ĺͲ�ɵó����ۣ�
��3����������������ù��ɶ��������������ʱ��t�����ɵó�����.
���:
��1��������ã�OD=OC=2��
��OE��CD��
��OEƽ�֡�COD��
���COE=![]() ��AOC=45�㣬
��AOC=45�㣬
��OC=CE=2��
��E��2��2������ֱ��OE�Ľ���ʽΪy=kx������E�������ã�2=2k��
��k=1��
��ֱ��OE�Ľ���ʽΪy=x��
��2����Rt��COE�У����ݹ��ɶ����ã�OE=2![]() ��
��
������ã��Ե�C��P��D��BΪ�����ͼ�����ı��Σ�
��t��![]() ��t
��t![]() ��
��
�����������
��OE��CD�Ľ���ΪM��
�ٵ���P��OM���˶�ʱ��0��t��![]() ��
��
S=S����OABC��S��POC��S��POD��S��DAB=8��![]() ��
��![]() ��2=��2
��2=��2![]() t+6��
t+6��
�ڵ���P��ME���˶�ʱ��![]() ��t��
��t��![]() ���Ե�C��P��D��BΪ������ı���Ϊ���ı��Σ����������⣬
���Ե�C��P��D��BΪ������ı���Ϊ���ı��Σ����������⣬
�۵�P��OE���ӳ������˶�ʱ��t��![]() ��
��
S=S��CDB+S��PCB=![]() =2
=2![]() t��
t��
S=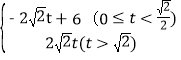 ��
��
��3�����ڣ����ɣ�PC2=��![]() t��2+��2��
t��2+��2��![]() t��2=4t2��4
t��2=4t2��4![]() t+4��PN2=��2��
t+4��PN2=��2��![]() t��2+��1��
t��2+��1��![]() t��2=4t2��6
t��2=4t2��6![]() t+5��NC2=5��
t+5��NC2=5��
�ٵ���CPN=90��ʱ��PC2+PN2=CN2��
��4t2��4![]() t+4+4t2��6
t+4+4t2��6![]() t+5=5��
t+5=5��
��t=![]() ��t=
��t=![]() ��
��
��P��![]() ��
��![]() ����2��2����
����2��2����
�ڵ���PNC=90��ʱ��CN2+PN2=PC2��
��5+4t2��6![]() t+5=4t2��4
t+5=4t2��4![]() t+4��
t+4��
��t=![]() ��
��
��P��3��3����
�۵���PCN=90��ʱ��PC2+CN2=PN2��4t2��4![]() t+4+5=4t2��6
t+4+5=4t2��6![]() t+5��
t+5��
��t=��![]() ����ʱ�����ڵ�P��
����ʱ�����ڵ�P��
����t=![]() ʱ��P��
ʱ��P��![]() ��
��![]() ����t=
����t=![]() ʱ��P��2��2����t=
ʱ��P��2��2����t=![]() ʱ��P��3��3����
ʱ��P��3��3����
�㾦: ������һ�κ����ۺ��⣬��Ҫ�����˽�ƽ���ߵ����ʣ�����ϵ����������ͼ�ε�����ļ��㷽�������ɶ��������ù��ɶ������������ǽⱾ��Ĺؼ�.