题目内容
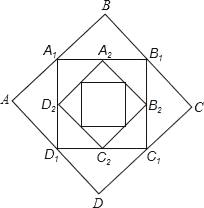
【题目】如图，正方形ABCD的边长为1，顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1，再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…，以此类推，则第2018个正方形A2018B2018C2018D2018的周长是_____．
【答案】
【解析】分析: 根据题意，利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半，根据面积关系可得周长关系，以此类推可得正方形A2018B2018C2018D2018的周长．
详解: 顺次连接正方形ABCD四边的中点得正方形A1B1C1D1，则得正方形A1B1C1D1的面积为正方形ABCD面积的一半，即
，则周长是原来的
；
顺次连接正方形A1B1C1D1中点得正方形A B C D ，则正方形A B C D 的面积为正方形A1B1C1D1面积的一半，即
，则周长是原来的；
顺次连接正方形A B C D 得正方形A B C D ，则正方形A B C D 的面积为正方形A B C D 面积的一半，即
，则周长是原来的
；
顺次连接正方形A B C D 中点得正方形A4B4C4D4，则正方形A4B4C4D4的面积为正方形A B C D 面积的一半
，则周长是原来的；
以此类推，则第2018个正方形A2018B2018C2018D2018的周长是4×
＝；
故答案是：.
点睛: 本题考查了利用了三角形的中位线的性质，相似图形的面积比等于相似比的平方的性质．进而得到周长关系．
练习册系列答案
走进文言文系列答案
相关题目
