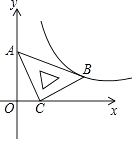题目内容
【题目】如图，直线y1=ax+b与双曲线y2= 
交于A、B两点，与x轴交于点C，点A的纵坐标为6，点B的坐标为（﹣3，﹣2）． 
（1）求直线和双曲线的解析式；
（2）求点C的坐标，并结合图象直接写出y1＜0时x的取值范围．
【答案】
（1）解：∵点B（﹣3，﹣2）在双曲线y2= 
上，
∴ 
，
∴k=6，
∴双曲线的解析式为y2= 
．
把y=6代入y2= 得：x=1，
∴A的坐标为（1，6），
∵直线y1=ax+b经过A、B两点，
∴ 
，解得： 
，
∴直线的解析式为直线y1=2x+4；
（2）解：由直线y1=0得，x=﹣2，
∴点C的坐标为（﹣2，0），
当y1＜0时x的取值范围是x＜﹣2．
【解析】（1）由点B的坐标求出k=6，得出双曲线的解析式为y2= ．求出A的坐标为（1，6），由点A和B的坐标以及待定系数法即可求出直线的解析式为直线y1=2x+4；（2）求出点C的坐标为（﹣2，0），即可得出当y1＜0时x的取值范围．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】下表给出了代数式x2+bx+c与x的一些对应值：
x | … | 0 | 1 | 2 | 3 | 4 | … |
x2+bx+c | … | 3 | ﹣1 | 3 | … |
（1）请在表内的空格中填入适当的数；
（2）设y=x2+bx+c，则当x取何值时，y＞0；
（3）请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象？
