题目内容
【题目】下表给出了代数式x2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
x2+bx+c | … | 3 | ﹣1 | 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
【答案】
(1)解:这个代数式属于二次函数.当x=0,y=3;x=4时,y=3.
说明此函数的对称轴为x=(0+4)÷2=2.那么﹣ ![]() =﹣
=﹣ ![]() =2,b=﹣4,经过(0,3),
=2,b=﹣4,经过(0,3),
∴c=3,二次函数解析式为y=x2﹣4x+3,
当x=1时,y=0;
当x=3时,y=0.
(2)解:由(1)可得二次函数与x轴的交点坐标,由于本函数开口向上,
可根据与x轴的交点来判断什么时候y>0.
当x<1或x>3时,y>0
(3)解:由(1)得y=x2﹣4x+3,即y=(x﹣2)2﹣1.
将抛物线y=x2﹣4x+3先向左平移2个单位,再向上平移1个单位即得抛物线y=x2.
【解析】根据与x轴的交点坐标得到什么时候y>0.讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可.
【考点精析】解答此题的关键在于理解二次函数图象的平移的相关知识,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.

 互动英语系列答案
互动英语系列答案【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°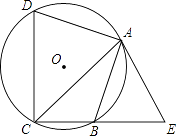
(1)求证:AE是⊙O的切线;
(2)若 AB=AD,AC=2 ![]() ,tan∠ADC=3,求CD的长.
,tan∠ADC=3,求CD的长.
【题目】某生物科技发展公司投资2000万元,研制出一种绿色保健食品.已知该产品的成本为40元/件,试销时,售价不低于成本价,又不高于180元/件.经市场调查知,年销售量y(万件)与销售单价x(元/件)的关系满足下表所示的规律.
销售单价x(元/件) | … | 60 | 65 | 70 | 80 | 85 | … |
年销售量y(万件) | … | 140 | 135 | 130 | 120 | 115 | … |
(1)y与x之间的函数关系式及自变量x的取值范围。
(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为W(万元)(W=年销售额﹣成本﹣投资),求出年销售量低于90万件和不低于90万件时,W与x之间的函数关系式;
(3)在(2)的条件下,当销售单位定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?