题目内容
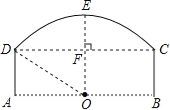
【题目】如图为一桥洞的形状,其正视图是由圆弧![]() 和矩形ABCD构成.O点为
和矩形ABCD构成.O点为![]() 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.
所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.
(1)求![]() 所在⊙O的半径DO;
所在⊙O的半径DO;
(2)若河里行驶来一艘正视图为矩形的船,其宽6米,露出水面AB的高度为h米,求船能通过桥洞时的最大高度h.
【答案】(1)5;(2)4.
【解析】
试题(1)利用垂径定理得出EO垂直平分CD,再利用勾股定理求出DO的长即可;
(2)利用垂径定理得出EO垂直平分MN,再利用勾股定理求出YO的长即可.
试题解析:(1)∵OE⊥弦CD于点F,CD为8米,EF为2米,
∴EO垂直平分CD,DF=4m,FO=DO﹣2(m),
在Rt△DFO中,![]() ,则
,则![]() ,解得:DO=5;
,解得:DO=5;
答:![]() 所在⊙O的半径DO为5m;
所在⊙O的半径DO为5m;
(2)如图所示:假设矩形的船为矩形MQRN,船沿中点O为中心通过,
连接MO,
∵MN=6m,∴MY=YN=3m,
在Rt△MOY中,![]() ,则
,则![]() ,解得:YO=4,
,解得:YO=4,
答:船能通过桥洞时的最大高度为4m.


练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目