题目内容
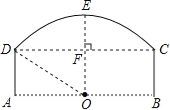
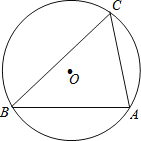
【题目】如图.在平行四边形纸片ABCD中，AC⊥AB，AC与BD相交于点O，将△ABC沿对角线AC折叠得到△AB'C.
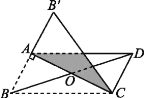
(1)求证：以A、C、D、B'为顶点的四边形是矩形
(2)若四边形ABCD的面积S=12cm，求阴影部分的面积.
【答案】（1）见解析；（2）阴影部分的面积是3.
【解析】
（1）连接B'D，由平行四边形的性质及折叠性质可得AB'=CD，∠BAC=∠B'AC，由AC⊥AB可证明B、A、B'共线，可得AB′//CD，可证明四边形ACDB'为平行四边形，根据有一个角是90°的平行四边形是矩形即可证明以A、C、D、B'为顶点的四边形是矩形；（2）设B'C与AD交于点E，根据矩形的性质可得AE=DE，由平行四边形的性质可得S△ACD=
S平行四边形ABCD，根据等底等高的三角形面积相等可得S△AEC=S△ACD，即可求出阴影部分面积.
(1)连接B'D.
∵在ABCD中，AB=CD，AB∥CD，△ABC沿对角线AC折叠，
∴AB'=CD，∠BAC=∠B'AC.
又∵AC⊥AB，
∴∠BAC=∠B'AC=90°，
∴B、A、B'在一条直线上，
∴AB'∥CD，
∴四边形ACDB'为平行四边形，
∵∠B'AC=90°，
∴以A、C、D、B'为顶点的四边形是矩形.
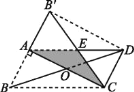
(2)设B'C与AD交于点E.
∵四边形ABCD是平行四边形，S平行四边形ABCD=12cm，
∴S△ACD=S平行四边形ABCD=×12=6，
∵四边形ACDB'为矩形，
∴AE=DE，
∴S△AEC=S△ACD=×6=3，即阴影部分的面积是3.
【题目】为了了解某校新初三暑期阅读课外书的情况，某研究小组随机采访该校新九年级的20位同学，得到这20位同学暑期读课外书册数的统计如下：
册数 | 0 | 2 | 3 | 5 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 8 | 2 | 2 | 1 |
（1）这20位同学暑期看课外书册数的中位数是 册，众数是 册,平均数是 册。
（2）若小明同学把册数中的数据“8”看成了“7”，那么中位数，众数，平均数中不受影响的是。
（3）若该校有600名新初三学生，试估计该校新初三学生暑期阅读课外书的总册数。
