Question

如图，直线y=-

3

3

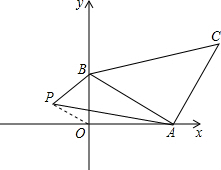
x+1与x轴、y轴分别交于A、B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°，如果在第二象限内有一点P（a，

1

2

），且△ABP的面积与△ABC的面积相等，求a的值．

Answer 1

连接PO，
由已知易得A（

3

，0），B（0，1），OA=

3

，
OB=1，AB=2，
∵等腰Rt△ABC中，∠BAC=90°，
∴S_△ABP=S_△ABC=2，
S_△AOP=

3

4

，S_△BOP=-

a

2

，
S_△ABP=S_△BOP+S_△AOB-S_△AOP=2，
即-

a

2

+

1

2

×

3

×1-

3

4

=2，
解得a=

3

2

-4．
答：a的值为a=

3

2

-4．