题目内容
在直角坐标系中,点A的坐标是(3,0),点P在第一象限内的直线y=-x +4上.设点P的坐标为(x,y).
+4上.设点P的坐标为(x,y).
(1)在所给的坐标系中画出直线y=-x+4;
(2)求△POA的面积S与变量x的函数关系式,并写出自变量x的取值范围;
(3)当S=
时,求点P的坐标,画出此时的△POA,并用尺规作图法,作出其外接圆(保留作图痕迹,不写作法).
 +4上.设点P的坐标为(x,y).
+4上.设点P的坐标为(x,y).(1)在所给的坐标系中画出直线y=-x+4;
(2)求△POA的面积S与变量x的函数关系式,并写出自变量x的取值范围;
(3)当S=
| 9 |
| 2 |
(本小题满分12分)
(1)直线y=-x+4分别交x轴、y轴于(4,0)(0,4);
如图所示:
(2)∵点P在第一象限,
∴点P的纵坐标y的绝对值|y|就是△POA的边OA上高的值,
∴S=
•OA•y=
y,即S=
y,
而点P为线段BC上一点,故y=-x+4,
∴S=
(-x+4)=-
x+6,
又而点P在线段BC上,自变量x的取值范围为:0<x<4
即所求S与变量x的函数关系式为:
S=-
x+6(0<x<4),
(3)若S=
,则有
=
y,y=3,
代入y=-x+4,得x=1,
∴点P的坐标为(1,3),
用尺规分别作出△POA的OA、OP(或AP)边的垂直平分线,
以两线交点为圆心、圆心到任一顶点为半径,作圆,即为△POA的外接圆(图形略).【以图形为准给分,不必写作法】

(1)直线y=-x+4分别交x轴、y轴于(4,0)(0,4);
如图所示:
(2)∵点P在第一象限,
∴点P的纵坐标y的绝对值|y|就是△POA的边OA上高的值,
∴S=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
而点P为线段BC上一点,故y=-x+4,
∴S=
| 3 |
| 2 |
| 3 |
| 2 |
又而点P在线段BC上,自变量x的取值范围为:0<x<4
即所求S与变量x的函数关系式为:

S=-
| 3 |
| 2 |
(3)若S=
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
代入y=-x+4,得x=1,
∴点P的坐标为(1,3),
用尺规分别作出△POA的OA、OP(或AP)边的垂直平分线,
以两线交点为圆心、圆心到任一顶点为半径,作圆,即为△POA的外接圆(图形略).【以图形为准给分,不必写作法】


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

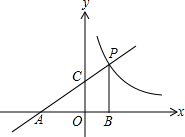 ⊥x轴,B为垂足,S△ABP=9.
⊥x轴,B为垂足,S△ABP=9. 坐标原点,△PAO的面积为S.
坐标原点,△PAO的面积为S.
 点,过P、C的直线l与AB及y轴围成△PBC,如图.
点,过P、C的直线l与AB及y轴围成△PBC,如图.

