题目内容
如图，把等腰直角△ABC放在直角坐标系内，其中∠CAB=90°，点A、B的坐标分别为（1，0）（4，0），将等腰直角△ABC沿x轴向右平移，当点C落在直线y=x-2上时，则等腰直角△ABC被直线y=x-2扫过的面积为______．
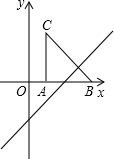
∵∠CAB=90°，点A、B的坐标分别为（1，0）、（4，0），
∴AC=3，BC=3
，
当点C落在直线y=x-2上时，如图，
故四边形BB′C′C是平行四边形，
则A′C′=AC=3，
把y=3代入直线y=x-2，
解得x=5，即OA′=5，
故AA′=BB′=4，
则平行四边形BB′C′C的面积=BB′×A′C′=4×3=12．
故答案为：12．
∴AC=3，BC=3
| 2 |
当点C落在直线y=x-2上时，如图，
故四边形BB′C′C是平行四边形，
则A′C′=AC=3，
把y=3代入直线y=x-2，
解得x=5，即OA′=5，
故AA′=BB′=4，
则平行四边形BB′C′C的面积=BB′×A′C′=4×3=12．
故答案为：12．
练习册系列答案
智能训练练测考系列答案
相关题目
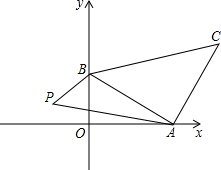
⊥x轴，B为垂足，S△ABP=9．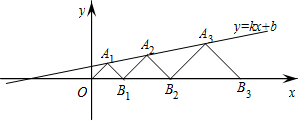
之间关系如图．
km的B处与爷爷相遇，求大刚下山时的速度．