题目内容
已知A、B是直线y=2x-2与x轴、y轴的交点，C在A正右边，D在B正上方，CA=2，DB=3，求C、D所在直线解析式．
∵A、B是直线y=2x-2与x轴、y轴的交点，
∴x=0，y=-2，B点坐标为：（0，-2），
y=0，x=1，A点坐标为：（1，0），
∵C在A正右边，CA=2，
∴点坐标为：（3，0），
∵D在B正上方，DB=3，
∴D点坐标为：（0，1），
将C，D代入解析式y=kx+b，
∴
，
解得：
，
∴C、D所在直线解析式为：y=-
x+1．
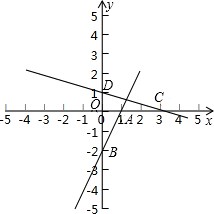
∴x=0，y=-2，B点坐标为：（0，-2），
y=0，x=1，A点坐标为：（1，0），
∵C在A正右边，CA=2，
∴点坐标为：（3，0），
∵D在B正上方，DB=3，
∴D点坐标为：（0，1），
将C，D代入解析式y=kx+b，
∴
|
解得：
|
∴C、D所在直线解析式为：y=-
| 1 |
| 3 |
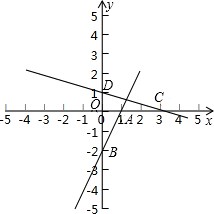
练习册系列答案
相关题目
⊥x轴，B为垂足，S△ABP=9．
y（元）是用水量x（吨）的函数，其函数图象如图所示．
坐标原点，△PAO的面积为S．
