题目内容
如图,已知:矩形ABCD中,AD=2,点E、F分别在边CD、AB上,且四边形AECF是菱形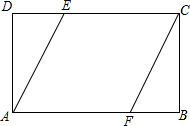 ,tan∠DAE=
,tan∠DAE=| 1 | 2 |
(1)DE的长;
(2)菱形AECF的面积?
分析:(1)直接根据三角函数公式即可求出DE的长;
(2)由DE的长,根据勾股定理求出AE的长,又AF=AE,再根据菱形的面积公式求解即可.
(2)由DE的长,根据勾股定理求出AE的长,又AF=AE,再根据菱形的面积公式求解即可.
解答:解:(1)∵点E在矩形ABCD的CD边上,
∴∠ADE=90°,
在直角三角形ADE中,∠ADE=90°,AD=2,tan∠DAE=
,
∴DE=AD•tan∠DAE=1,
∴AE=
=
.
(2)∵四边形AECF是菱形,
∴AF=AE=
,
又∵AD⊥AF,
∴S菱形AECF=AD•AF=2×
=2
.(2分)
∴∠ADE=90°,
在直角三角形ADE中,∠ADE=90°,AD=2,tan∠DAE=
| 1 |
| 2 |
∴DE=AD•tan∠DAE=1,
∴AE=
| AD2+DE2 |
| 5 |
(2)∵四边形AECF是菱形,
∴AF=AE=
| 5 |
又∵AD⊥AF,
∴S菱形AECF=AD•AF=2×
| 5 |
| 5 |
点评:本题考查了矩形、菱形的性质,同时考查了勾股定理及解直角三角形的知识,难度不大,注意这些知识的灵活运用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
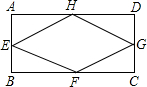 如图,已知在矩形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.若sin∠AEH=
如图,已知在矩形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.若sin∠AEH=| 12 |
| 13 |
| A、240 | B、60 |
| C、120 | D、169 |

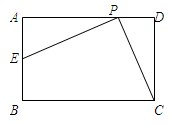 连接PC,过点P作PE⊥PC交AB于E
连接PC,过点P作PE⊥PC交AB于E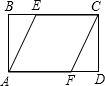 如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.
如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.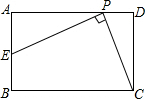 (2011•绍兴县模拟)如图,已知在矩形ABCD中,AB=4,BC=6,P是线段AD上的任意一点(不含端点A、D),连接PC,过点P作PE⊥PC交AB于E,则BE的取值范围是( )
(2011•绍兴县模拟)如图,已知在矩形ABCD中,AB=4,BC=6,P是线段AD上的任意一点(不含端点A、D),连接PC,过点P作PE⊥PC交AB于E,则BE的取值范围是( )