题目内容
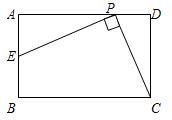
如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),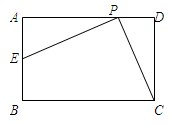 连接PC,过点P作PE⊥PC交AB于E
连接PC,过点P作PE⊥PC交AB于E(1)求证:△AEP∽△DPC;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,设DP=x,BE=y,求y与x之间的函数关系式,并求出x的取值范围.
分析:(1)利用矩形的性质可以得到∠A=∠D,利用PE⊥PC可以得到∠APE=∠DCP,从而证明两三角形相似;
(2)利用上题证得的三角形相似,列出比例式,进而得到两个变量之间的函数关系.
(2)利用上题证得的三角形相似,列出比例式,进而得到两个变量之间的函数关系.
解答:解:(1)∵四边形ABCD为矩形,
∴∠A=∠D,
∴∠AEP+∠APE=90°,
∵PE⊥PC
∴∠APE+∠CPD=90°,
∴∠AEP=∠DPC,
∴△AEP∽△DPC;
(2)设DP=x,BE=y,则AE=2-y,AP=3-x,
∵△AEP∽△DPC
∴
=
,
即:
=
,
整理得:y=
x2-
x+2(0<x<3).
∴∠A=∠D,
∴∠AEP+∠APE=90°,
∵PE⊥PC
∴∠APE+∠CPD=90°,
∴∠AEP=∠DPC,
∴△AEP∽△DPC;
(2)设DP=x,BE=y,则AE=2-y,AP=3-x,
∵△AEP∽△DPC
∴
| DC |
| AP |
| PD |
| AE |
即:
| 2 |
| 3-x |
| x |
| 2-y |
整理得:y=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了相似三角形的判定及性质,正确的利用矩形的性质是解题的关键.

练习册系列答案
相关题目
 自选题:
自选题: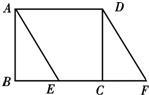 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.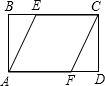 如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.
如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积. 如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=
如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=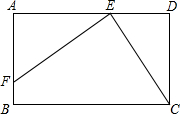 E=3cm,BC=7cm.
E=3cm,BC=7cm.