题目内容
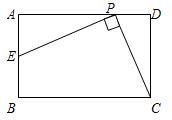
如图，已知在矩形ABCD中，AB=4，AD=6，经过点A作一直线交边BC于点E，并把矩形分成两部分，一是直角梯形，一是直角三角形，若梯形的面积与直角三角形的面积之比为3：1，则BE的长为
分析：根据题意得S△ABE=
S矩形ABCD，据此求解．
| 1 |
| 4 |
解答：解：∵梯形的面积与直角三角形的面积之比为3：1，
∴S△ABE=
S矩形ABCD，即
×4×BE=
×4×6．
∴BE=3．
∴S△ABE=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴BE=3．
点评：解决本题需注意利用所给的面积比得三角形的面积与已知矩形的面积之间的关系．
练习册系列答案
相关题目
自选题：
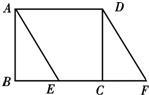如图，已知在矩形ABCD中，AB=3，点E在BC上且∠BAE=30°，延长BC到点F使CF=BE，连接DF．
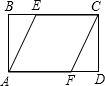如图，已知在矩形ABCD中，AB=2，BC=4，四边形AFCE为菱形，求菱形的面积．
如图，已知在矩形ABCD中，AB=6，BC=8，⊙E和⊙F分别是△ABC和△ADC的内切圆，与对角线AC分别切于E、F，则EF=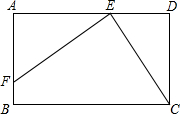
E=3cm，BC=7cm．