题目内容
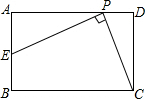（2011•绍兴县模拟）如图，已知在矩形ABCD中，AB=4，BC=6，P是线段AD上的任意一点（不含端点A、D），连接PC，过点P作PE⊥PC交AB于E，则BE的取值范围是（ ）分析：由于BE的最大值为AB的长即2，因此只需求得BE的最小值即可；设AP=x，AE=y，根据△AEP∽△DPC可得AP•PD=AE•CD，用x、y表示出其中的线段，即可得到关于x、y的函数关系式，根据函数的性质即可求得y的最大值，由此可求得BE的最小值，即可得到BE的取值范围．
解答：解：∵四边形ABCD为矩形，
∴∠A=∠D，
∴∠AEP+∠APE=90°，
∵PE⊥PC
∴∠APE+∠CPD=90°，
∴∠AEP=∠DPC，
∴△AEP∽△DPC；
设DP=x，BE=y，则AE=4-y，AP=6-x，
∵△AEP∽△DPC，
∴
=
，代入整理可得：y=
x2-
x+4=
（x-3）2+
，
故BE的最小值为
，又因为BE的最大值为4，
∴BE的范围为
≤BE＜4．
故选B．
∴∠A=∠D，
∴∠AEP+∠APE=90°，
∵PE⊥PC
∴∠APE+∠CPD=90°，
∴∠AEP=∠DPC，
∴△AEP∽△DPC；
设DP=x，BE=y，则AE=4-y，AP=6-x，
∵△AEP∽△DPC，
∴
| CD |
| PA |
| PD |
| EA |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
故BE的最小值为
| 7 |
| 4 |
∴BE的范围为
| 7 |
| 4 |
故选B．
点评：此题主要考查的是矩形的性质、相似三角形的判定和性质以及二次函数最值的应用，关键是证明△AEP∽△DPC，这一点不容易想到，难度较大，另外要求我们熟练掌握二次函数的最值的求解办法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2011•绍兴县模拟）如图，菱形ABCD的周长为16，以AB为一边画等边△ABE，点E、D在直线AB的同侧，在AC上找一点P，使EP+DP最小，则这个最小值为
接EF并延长EF交AB于G，且EG⊥AB．
（2011•绍兴县模拟）已知菱形OABC中，A（0，5），B（3，1），连接AC交x轴于M，线段OA上有一动点P，以每秒1个单位的速度从点O出发向线段的另一端点A运动，到点A后停止运动，运动时间为t秒，过P作PE⊥AC交AB于E，连接PB、BM（如图1）