题目内容
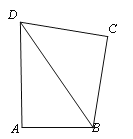
【题目】如图,在四边形ABCD中,AB=1,AD=![]() ,BD=2,∠ABC+∠ADC=180°,CD=
,BD=2,∠ABC+∠ADC=180°,CD=![]() .
.
(1)判断△ABD的形状,并说明理由;
(2)求BC的长.
【答案】(1)△ABD是直角三角形.理由见解析;(2)![]() .
.
【解析】
(1)根据勾股定理的逆定理即可证得△ABD是直角三角形;
(2)根据四边形内角和定理可证得![]() 是直角三角形,再根据勾股定理即可求得答案.
是直角三角形,再根据勾股定理即可求得答案.
(1)△ABD是直角三角形.
理由如下:在△ABD中,
∵AB2+AD2=12+(![]() )2=4,
)2=4,
BD2=22=4,
∴AB2+AD2=BD2.
∴△ABD是直角三角形.
(2) 在四边形ABCD中,
∵∠ABC+∠ADC=180°,
∴∠A+∠C=180°.
由(1)得∠A=90°,∴∠C=90°.
在![]() 中,∠C=90°,
中,∠C=90°,
BC2=BD2-CD2=22-(![]() )2=2.
)2=2.
∴BC=![]() .
.

练习册系列答案
相关题目