Question

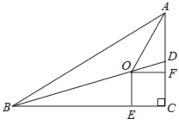
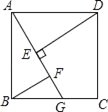
【题目】如图，ABCD是正方形， G是BC上（除端点外）的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F．给出以下结论：①△AED≌△BFA；②DE﹣BF=EF；③△BGF∽△DAE；④DE﹣BG=FG．其中正确的有（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】

由四边形ABCD是正方形，可得AB=AD，由DE⊥AG，BF∥DE，易证得BF⊥AG，又由同角的余角相等，可证得∠BAF=∠ADE，则可利用AAS判定△AED≌△BFA；由全等三角形的对应边相等，易证得DE-BF=EF；有两角对应相等的三角形相似，可证得△BGF∽△DAE；利用排除法即可求得答案．

解：∵四边形ABCD是正方形，
∴AB=AD，AD∥BC，
∵DE⊥AG，BF∥DE，
∴BF⊥AG，
∴∠AED=∠DEF=∠BFE=90°，
∵∠BAF+∠DAE=90°，∠DAE+∠ADE=90°，
∴∠BAF=∠ADE，
∴△AED≌△BFA（AAS）；故A正确；
∴DE=AF，AE=BF，
∴DE-BF=AF-AE=EF，故B正确；
∵AD∥BC，
∴∠DAE=∠BGF，
∵DE⊥AG，BF⊥AG，
∴∠AED=∠GFB=90°，
∴△BGF∽△DAE，故C正确；
∵DE，BG，FG没有等量关系，
故不能判定DE-BG=FG正确．故D错误（也可以用排除法判断）；

故选：C．