Question

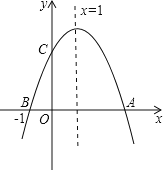
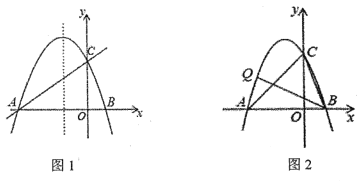
【题目】如图，已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线，且抛物线经过B(1，0)，C(0，3)两点，与x轴交于点A.

（1）求抛物线的解析式；

（2）如图1，在抛物线的对称轴直线上找一点M，使点M到点B的距离与到点C的距离之和最小，求出点M的坐标；

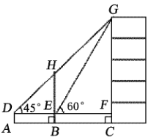
（3）如图2，点Q为直线AC上方抛物线上一点，若∠CBQ=45°，请求出点Q坐标.

Answer 1

【答案】（1）；（2）当点到点的距离与到点的距离之和最小时的坐标为；（3）点.

【解析】

（1）根据对称轴方程可得，把B、C坐标代入列方程组求出a、b、c的值即可得答案；

（2）根据二次函数的对称性可得A点坐标，设直线AC与对称轴的交点为M，可得MB=MA，即可得出MB+MC=MC+MA=AC，为MB+MC的最小值，根据A、C坐标，利用待定系数法可求出直线AC的解析式，把x=-1代入求出y值，即可得点M的坐标.

（3）设直线BQ交y轴于点H，过点作于点，利用勾股定理可求出BC的长，根据∠CBQ=45°可得HM=BM，利用∠OCB的正切函数可得CM=3HM，即可求出CM、HM的长，利用勾股定理可求出CH的长，即可得H点坐标，利用待定系数法可得直线BH的解析式，联立直线BQ与抛物线的解析式求出交点坐标即可得点Q坐标.

（1）∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线，

∴，

∵抛物线经过B(1，0)，C(0，3)两点，

∴，

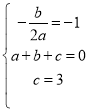解得：，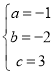

∴抛物线解析式为.

（2）设直线AC的解析式为y=mx+n，

∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线，B（0，0），

∴点A坐标为（-3，0），

∵C（0，3），

∴，

解得：，

∴直线解析式为，

设直线与对称轴的交点为，

∵点A与点B关于对称轴x=-1对称，

∴MA=MB，

∴MB+MC=MA+MC=AC，

∴此时的值最小，

当时，y=-1+3=2，

∴当点到点的距离与到点的距离之和最小时的坐标为.

（3）如图，设直线交轴于点，过点作于点，

∵B（1，0），C（0，3），

∴OB=1，OC=3，BC==，

∴，

∵∠CBQ=45°，

∴△BHM是等腰直角三角形，

∴HM=BM，

∵tan∠OCB=，

∴CM=3HM，

∴BC=MB+CM=4HM=，

解得：，

∴CM=，

∴CH==，

∴OH=OC-CH=3-=，

∴，

设直线BH的解析式为：y=kx+b，

∴，

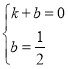解得：，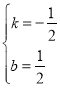

∴的表达式为：，

联立直线BH与抛物线解析式得，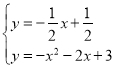

解得：（舍去）或x=，

当x=时，y==，

∴点Q坐标为（，）.