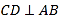题目内容
【题目】如图,△![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,
,![]() ∥
∥![]() ,
,![]() ,下列结论错误的是( )
,下列结论错误的是( )
A.![]() 30°B.
30°B.![]()
C.△![]() 的周长为10D.△
的周长为10D.△![]() 的周长为9
的周长为9
【答案】C
【解析】
根据等边三角形的性质和直角三角形两锐角互余的性质可判断A;
根据30°角的直角三角形的性质可判断B;
由B的结论结合![]() 为
为![]() 的中点可求出AB的长,进而可判断C;
的中点可求出AB的长,进而可判断C;
由![]() ∥
∥![]() 可判断△CEF是等边三角形,再求出CE的长即可判断D.
可判断△CEF是等边三角形,再求出CE的长即可判断D.
解:∵△![]() 是等边三角形,
是等边三角形,
∴AB=AC=BC,∠A=∠B=∠C=60°,
∵![]() ,∴∠AED=90°,
,∴∠AED=90°,
∴∠ADE=90°-∠A=30°,所以A正确;
∵AE=1,∠ADE=30°,∴AD=2AE=2,所以B正确;
∵![]() 为
为![]() 的中点,∴AB=2AD=4,∴△
的中点,∴AB=2AD=4,∴△![]() 的周长为4×3=12,所以C错误;
的周长为4×3=12,所以C错误;
∵![]() ∥
∥![]() ,
,
∴∠CEF=∠A=60°,∠CFE=∠B=60°,
∴△CEF是等边三角形,
∵AE=1,∴CE=AC-AE=3,
∴△![]() 的周长为9,所以D正确.
的周长为9,所以D正确.
故选C.

【题目】某班50名学生的身高如下(单位:cm):
160 163 152 161 167 154 158 171 156 168
178 151 156 154 165 160 168 155 162 173
158 167 157 153 164 172 153 159 154 155
169 163 158 150 177 155 166 161 159 164
171 154 157 165 152 167 157 162 155 160
(1)小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本:161,155,174,163,152,请你计算小丽所抽取的这个样本的平均数;
(2)小丽将这50个数据按身高相差4cm分组,并制作了如下的表格:
身高 | 频数 | 频率 |
147.5~151.5 |
| 0.06 |
151.5~155.5 |
|
|
155.5~159.5 | 11 | m |
159.5~163.5 |
| 0.18 |
163.5~167.5 | 8 | 0.16 |
167.5~171.5 | 4 |
|
171.5~175.5 | n | 0.06 |
175.5~179.5 | 2 |
|
合计 | 50 | 1 |
①m= ,n= ;
②这50名学生身高的中位数落在哪个身高段内?身高在哪一段的学生数最多?