题目内容
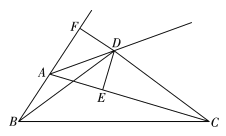
【题目】如图所示,已知 AD//BC, 点 E 为 CD 上一点,AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证:(1)△ABE≌△AEF;(2) AD+BC=AB

【答案】见解析
【解析】
(1)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据两直线平行,内错角相等可得∠2=∠F,然后求出∠1=∠F,再利用“角角边”证明△ABE和△AFE全等即可;
(2)根据全等三角形对应边相等可得BE=FE,然后利用“角边角”证明△BCE和△FDE全等,根据全等三角形对应边相等可得BC=DF,然后根据AD+BC整理即可得证.
 (1)证明:如图,∵AE、BE分别平分∠DAB、∠CBA,
(1)证明:如图,∵AE、BE分别平分∠DAB、∠CBA,
∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠2=∠F,∠1=∠F,
在△ABE和△AFE中,

∴△ABE≌△AFE(AAS);
(2)证明:∵△ABE≌△AFE,
∴BE=EF,
在△BCE和△FDE中,

∴△BCE≌△FDE(ASA),
∴BC=DF,
∴AD+BC=AD+DF=AF=AB,
即AD+BC=AB.

练习册系列答案
相关题目