��Ŀ����
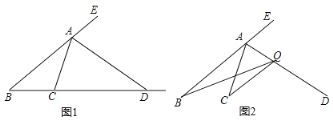
����Ŀ����ͼ��ֱ��EF��GH����B��A�ֱ���ֱ��EF��GH�ϣ�����AB����AB�����������ABC�����С�ACB��90�����ҡ�DAB����BAC��ֱ��BDƽ�֡�FBC��ֱ��GH��D
(1) ����Cǡ��EF�ϣ���ͼ1�����DBA��_________
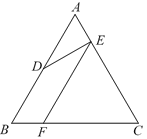
(2) ��A�������ƶ��������������䣬��ͼ2����1���еĽ��ۻ���������������֤����Ľ��ۣ�����������˵���������
(3) ������Ŀ��������ACB��90��������Ϊ������ACB��120�����������������䣬��ô��DBA��_________��ֱ��д�����������֤����
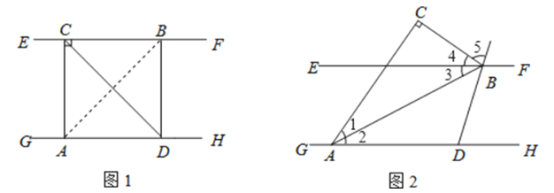
���𰸡�(1)45��;(2)������;(3)60��.
��������
��1��������ֱ��ƽ�У�ͬ���ڽǻ��������CAD=90����Ȼ�������BAC=45�����Ӷ��õ���ABC=45�����ٸ���BDƽ�֡�FBC�����DBC=90����Ȼ����⼴�ɣ�
��2��������ֱ��ƽ�У��ڴ�����ȿɵá�2=��3���ٸ��������ε��ڽǺͶ�����ʾ����4��Ȼ���ʾ��5��������ƽ�ǵ���180����ʽ��ʾ����DBA�������ɵý⣻
��3�����ݣ�2���Ľ��ۼ��㼴�ɵý⣮
�⣺��1����EF��GH��
���CAD=180��-��ACB=180��-90��=90����
�ߡ�DAB=��BAC��
���BAC=45����
���ABC=45����
��BDƽ�֡�FBC��
���DBC=![]() ��180��=90����
��180��=90����
���DBA=90��-45��=45����
��2���⣺��ͼ�����DAB=��BAC=x������1=��2=x��
��EF��GH��
���2=��3��
����ABC�ڣ���4=180��-��ACB-��1-��3=180��-��ACB-2x��
��ֱ��BDƽ�֡�FBC��
���5=![]() ��180��-��4��=
��180��-��4��=![]() ��180��-180��+��ACB+2x��=
��180��-180��+��ACB+2x��=![]() ��ACB+x��
��ACB+x��
���DBA=180��-��3-��4-��5��
=180��-x-��180��-��ACB-2x��-��![]() ��ACB+x����
��ACB+x����
=180��-x-180��+��ACB+2x-![]() ��ACB-x��
��ACB-x��
=![]() ��ACB��
��ACB��
=![]() ��90����
��90����
=45����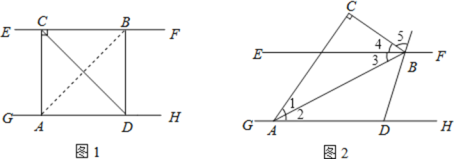
��3���ɣ�2����֪����ACB=120��ʱ��
��DBA=![]() ��120��=60����
��120��=60����

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д�