Question

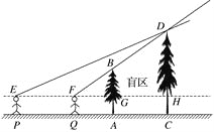
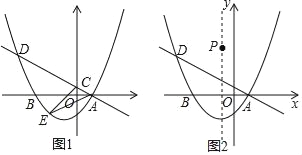
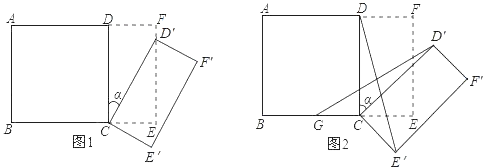
【题目】如图1所示，将一个边长为2的正方形ABCD和一个长为2，宽为1的矩形CEFD拼在一起，构成一个大的矩形ABEF，现将小矩形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为α．

（1）当点D′恰好落在EF边上时，求旋转角α的值；

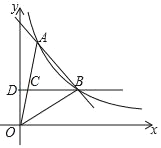
（2）如图2，G为BC中点，且0°＜α＜90°，求证：GD′＝E′D．

Answer 1

【答案】（1）∠α＝30°；（2）详见解析.

【解析】

（1）根据旋转的性质得CD′＝CD＝2，在Rt△CED′中，CD′＝2，CE＝1，则∠CD′E＝30°，然后根据平行线的性质即可得到∠α＝30°；（2）由G为BC中点可得CG＝CE，根据旋转的性质得∠D′CE′＝∠DCE＝90°，CE＝CE′CE，则∠GCD′＝∠DCE′＝90°+α，然后根据“SAS”可判断△GCD′≌△E′CD，则GD′＝E′D．

（1）解：∵长方形CEFD绕点C顺时针旋转至CE′F′D′，

∴CD′＝CD＝2，

在Rt△CED′中，CD′＝2，CE＝1，

∴∠CD′E＝30°，

∵CD∥EF，

∴∠α＝30°；

（2）证明：∵G为BC中点，

∴CG＝1，

∴CG＝CE，

∵长方形CEFD绕点C顺时针旋转至CE′F′D′，

∴∠D′CE′＝∠DCE＝90°，CE＝CE′＝CG，

∴∠GCD′＝∠DCE′＝90°+α，

在△GCD′和△E′CD中

，

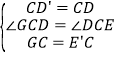∴△GCD′≌△E′CD（SAS），

∴GD′＝E′D．