题目内容
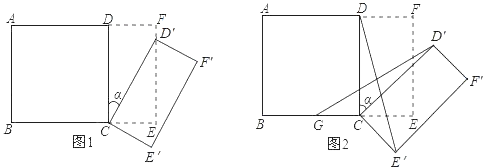
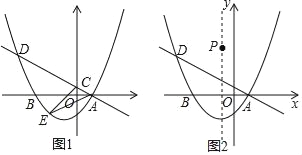
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
(1)求抛物线的函数表达式;
(2)当点D在第二象限且满足CD=5AC时,求直线l的解析式;
(3)在(2)的条件下,点E为直线l下方抛物线上的一点,直接写出△ACE面积的最大值;
(4)如图2,在抛物线的对称轴上有一点P,其纵坐标为4,点Q在抛物线上,当直线l与y轴的交点C位于y轴负半轴时,是否存在以点A,D,P,Q为顶点的平行四边形?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
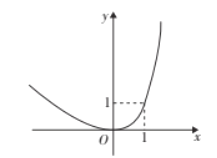
【答案】(1)y=![]() x2+x﹣
x2+x﹣![]() ;(2)y=﹣x+1;(3)当x=﹣2时,最大值为
;(2)y=﹣x+1;(3)当x=﹣2时,最大值为![]() ;(4)存在,点D的横坐标为﹣3或
;(4)存在,点D的横坐标为﹣3或![]() 或﹣
或﹣![]() .
.
【解析】
(1)设二次函数的表达式为:y=a(x+3)(x﹣1)=ax2+2ax﹣3a,即可求解;
(2)OC∥DF,则![]() 即可求解;
即可求解;
(3)由S△ACE=S△AME﹣S△CME即可求解;
(4)分当AP为平行四边形的一条边、对角线两种情况,分别求解即可.
(1)设二次函数的表达式为:y=a(x+3)(x﹣1)=ax2+2ax﹣3a,
即:![]() 解得:
解得:![]()
故函数的表达式为: ![]() ①;
①;
(2)过点D作DF⊥x轴交于点F,过点E作y轴的平行线交直线AD于点M,
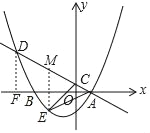
∵OC∥DF,∴![]() OF=5OA=5,
OF=5OA=5,
故点D的坐标为(﹣5,6),
将点A、D的坐标代入一次函数表达式:y=mx+n得:![]() ,解得:
,解得:![]()
即直线AD的表达式为:y=﹣x+1,
(3)设点E坐标为![]() 则点M坐标为
则点M坐标为![]()
则![]()
![]()
∵![]() 故S△ACE有最大值,
故S△ACE有最大值,
当x=﹣2时,最大值为![]() ;
;
(4)存在,理由:
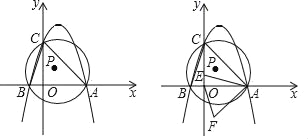
①当AP为平行四边形的一条边时,如下图,
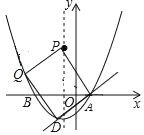
设点D的坐标为![]()
将点A向左平移2个单位、向上平移4个单位到达点P的位置,
同样把点D左平移2个单位、向上平移4个单位到达点Q的位置,
则点Q的坐标为![]()
将点Q的坐标代入①式并解得:![]()
②当AP为平行四边形的对角线时,如下图,
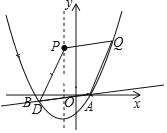
设点Q坐标为![]() 点D的坐标为(m,n),
点D的坐标为(m,n),
AP中点的坐标为(0,2),该点也是DQ的中点,
则: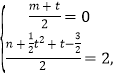 即:
即: 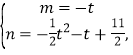
将点D坐标代入①式并解得:![]()
故点D的横坐标为:![]() 或
或![]() 或
或![]() .
.