Question

【题目】如图，S为一个点光源，照射在底面半径和高都为2m的圆锥体上，在地面上形成的影子为EB，且∠SBA=30°。（以下计算结果都保留根号）

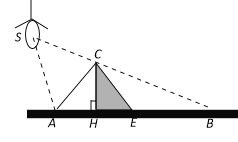
（1）、求影子EB的长；

（2）、若∠SAC=60°，求光源S离开地面的高度。

Answer 1

【答案】（1）、；（2）、2+

【解析】

试题分析：（1）、根据题意得出CH=HE=2m；根据∠SBA=30°得出HB=，从而根据BE=BH-HE得出答案；（2）、作CD⊥SA于点D，根据Rt△ACD的三角函数得出CD的长度，然后得出∠DSC的度数，从而求出SC的长度，最后求出SB的长度，根据SF=SB得出答案.

试题解析：（1）、∵圆锥的底面半径和高都为2m，

∴CH=HE=2m，

∵∠SBA=30°，

∴HB=m，

∴影长BE=BH﹣HE=（m）；

（2）、作CD⊥SA于点D，

在Rt△ACD中，得CD=ACcos30°=AC=，

∵∠SBA=30°，∠SAB=∠SAC+∠BAC=60°+45°=105°，

∴∠DSC=45°，∴SC=，

∴SB=2+BC=2+4，

∴SF=SB=（+2）m，

答：光源S离开地面的高度为（2+）m。