题目内容
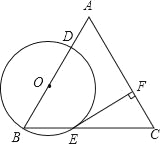
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)连接![]() 欲证直线
欲证直线![]() 是
是![]() 的切线,只需证明
的切线,只需证明![]() .利用等边三角形的三个内角都是60°、等腰
.利用等边三角形的三个内角都是60°、等腰![]() 以及三角形的内角和定理求得同位角
以及三角形的内角和定理求得同位角![]() 从而判定
从而判定![]() ,所以由已知条件
,所以由已知条件![]() 判定
判定![]() 即直线
即直线![]() 是
是![]() 的切线;
的切线;
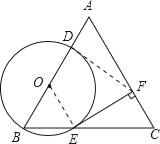
(2)连接![]() 设
设![]() 的半径是
的半径是![]() .由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于
.由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于![]() 的方程
的方程![]() ,解方程即可.
,解方程即可.
试题解析:(1)证明:连接![]()
![]() 是等边三角形,
是等边三角形,
![]()
在![]() 中,
中,![]()
![]()
![]()
![]() (同位角相等,两直线平行);
(同位角相等,两直线平行);
![]()
![]() 即直线
即直线![]() 是
是![]() 的切线;
的切线;
(2)连接![]()
![]() 与
与![]() 相切,
相切,
![]()
设![]() 的半径是
的半径是![]() ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
解得,![]()
![]() 的半径是
的半径是![]()

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目