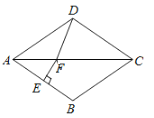
题目内容
【题目】已知二次函数y=-x 2 +2mx-m 2+4
(1)当m=1时,抛物线的对称轴和顶点坐标:
(2)求证:不论m取何值时该二次函数的图像与x轴必有两个不同交点
(3)若该二次函数的图像与x轴交于点A, B(点A在点B的左侧),顶点为C,则这时△ABC的面积为
【答案】(1)对称轴为x=1,顶点坐标为(1,4);(2)证明见解析;(3)8.
【解析】
(1)把m=1代入到二次函数解析式中,用配方法整理成顶点式,即可得到其对称轴和顶点坐标;
(2)应用根的判别式即可证明;
(3)令y=0,求出A、B横坐标,用m表示顶点C坐标,求△ABC面积.
(1)把m=1代入到y=-x 2 +2mx-m 2+4中,
得y=-x 2 +2x+3=-(x-1)2+4,
所以对称轴为x=1,顶点坐标为(1,4);
(2)当y=0时,-x2+2mx-m2+4=0,
∵b2-4ac=4m2-4×(-1)×(-m2+4)=16>0,
∴此一元二次方程有两个不相等的实数根,
∴该二次函数的图象与x轴必有两个不同交点;
(3)当y=0时,-x2+2mx-m2+4=0,
解得:x1=m+2,x2=m-2,
∵点A在点B的左侧,
∴点A、B横坐标分别为m-2,m+2,
∴AB=4,
配方得y=-x2+2mx-m2+4=-(x-m)2+4,
∴抛物线顶点为(m,4)
∴S△ABC=![]() ×4×4=8,
×4×4=8,
故答案为:8.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.