题目内容
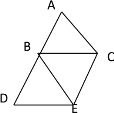
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,求BF的长;
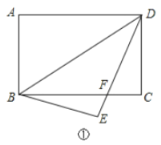
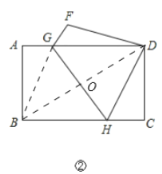
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.

【答案】(1)![]()
(2)![]()
【解析】
(1)根据折叠的性质可得∠ADB=∠EDB,再根据两直线平行,内错角相等可得∠ADB=∠DBC,然后求出∠FBD=∠FDB,根据等角对等边可得BF=DF,设BF=x,表示出CF,在Rt△CDF中,利用勾股定理列出方程求解即可;
(2)根据折叠的性质可得DH=BH,设BH=DH=x,表示出CH,然后在Rt△CDH中,利用勾股定理列出方程求出x,再连接BD、BG,根据翻折的性质可得
(1) 由折叠得,∠ADB=∠EDB,
∵矩形ABCD的对边AD∥BC,
∴∠ADB=∠DBC,
∴∠FBD=∠FDB,
∴BF=DF,
设BF=x,则CF=8x,
在Rt△CDF中,![]()
即![]()
解得x=![]()
故答案:![]()
(2)由折叠得,DH=BH,设BH=DH=x,
则CH=8x,
在Rt△CDH中, ![]()
即![]()
解得x=![]()
连接BD、BG,
由翻折的性质可得,BG=DG,∠BHG=∠DHG,
∵矩形ABCD的边AD∥BC,
∴∠BHG=∠DGH,
∴∠DHG=∠DGH,
∴DH=DG,
∴BH=DH=DG=BG,
∴四边形BHDG是菱形,
在Rt△BCD中,
S菱形BHDG=![]() BDGH=BHCD,
BDGH=BHCD,
即![]() ×10GH=
×10GH=![]() ×6,解得GH=
×6,解得GH=![]() .
.
故答案:![]()

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目