题目内容
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,DE⊥BD交AB于点E,设⊙O是△BDE的外接圆.
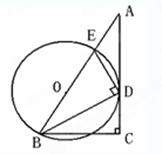
(1)求证:AC是⊙O的切线;
(2)求证: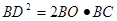 .
.

(1)求证:AC是⊙O的切线;
(2)求证:
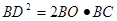 .
.26:(1)说明∠ODC=90度∵OD是⊙O的半径,∴AC是⊙O的切线. (2)说明△EDB相似于△DCB即可。
试题分析:(1)证明:连接OD,∵DE⊥DB,⊙O是△BDE的外接圆,
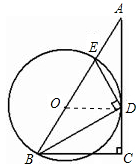
∴BE是直径,点O是BE的中点,
∵∠C=90°,∴∠DBC+∠BDC=90°,又BD为∠ABC的平分线,∴∠ABD=∠DBC,
∵OB=OD,∴∠ABD=∠ODB,则∠ODB+∠BDC=90°即∠ODC=90°
又∵OD是⊙O的半径,∴AC是⊙O的切线.
(2)依题意知,Rt△EDB和Rt△DCB中,∠EDB=∠C=90°。因为DB平分∠ABC,所以∠ABD=∠DBC。
所以Rt△EDB∽Rt△DCB。则
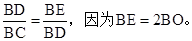 所以可得
所以可得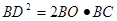
点评:本题难度中等,主要考查学生对圆与相似三角形性质知识点的掌握,为中考常考题型,注意数形结合应用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






 ,OC=1,则OB的长为 .?
,OC=1,则OB的长为 .?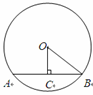

 B.
B.  C.
C.  D.
D. 


 ,DE=2,求AD的长.
,DE=2,求AD的长.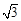 ,则阴影部分图形的面积为 .
,则阴影部分图形的面积为 .