题目内容
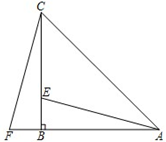
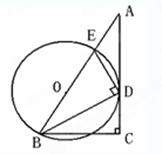
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.

(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:
(3)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.

(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:

(3)若tanC=
 ,DE=2,求AD的长.
,DE=2,求AD的长.(1)证明∠EDO=∠EBO=90°,所以DE与⊙O相切 (2)通过证明AC="2OE" ,BC2=CD·AC得BC2=2CD·OE (3)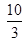
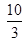
试题分析:(1) DE与⊙O相切

理由如下:连接OD,BD,
∵AB是直径,∴∠ADB=∠BDC=90°
∵E是BC的中点,∴DE=BE=CE,∴∠EDB=∠EBD,
∵OD=OB,∴∠OBD=∠ODB.
∴∠EDO=∠EBO=90°
∴DE与⊙O相切
(2)证明:由题意得OE是的
 ABC的中位线,∴AC=2OE
ABC的中位线,∴AC=2OE ∵∠ABC=∠BDC=900,∠C=∠C ,∴
 ABC∽
ABC∽ BDC
BDC∴
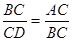 ,∴BC2=CD·AC,∴BC2=2CD·OE
,∴BC2=CD·AC,∴BC2=2CD·OE (3) ∵DE=2 BC=4 AB=4. tanC

tanA=
 , 设BD=AD
, 设BD=AD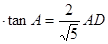 ,
,
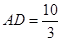
点评:本题考查直线与圆相切,相似三角形,三角函数,要求学生掌握直线与圆相切,会证明直线与圆相切,熟悉相似三角形的判定方法,会证明两个三角形相似

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
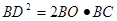 .
.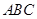 内接于⊙
内接于⊙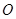 ,若⊙
,若⊙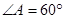 ,则
,则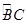 的长为____.
的长为____.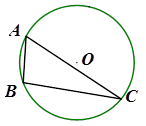

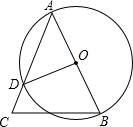
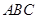 内接于
内接于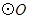 ,
,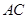 是
是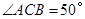 ,点D是弧BAC上一点,则
,点D是弧BAC上一点,则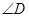 = °.
= °.
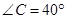 ,则∠AOB的度数为
,则∠AOB的度数为