题目内容
如图,AB是⊙O的直径,C是AB延长线上一点,点D在⊙O上,且∠A=30°,∠ABD=2∠BDC .

(1)求证:CD是⊙O的切线;
(2)过点O作OF∥AD,分别交BD、CD于点E、F.若OB =2,求 OE和CF的长.

(1)求证:CD是⊙O的切线;
(2)过点O作OF∥AD,分别交BD、CD于点E、F.若OB =2,求 OE和CF的长.
(1)连结OD,根据圆周角定理可得∠ADB=90°,即可求得∠ABD=60°,从而可以求得∠BDC= ,即可证得△ODB是等边三角形,则可得∠ODC=90°,问题得证;(2)
,即可证得△ODB是等边三角形,则可得∠ODC=90°,问题得证;(2) ,
,
 ,即可证得△ODB是等边三角形,则可得∠ODC=90°,问题得证;(2)
,即可证得△ODB是等边三角形,则可得∠ODC=90°,问题得证;(2) ,
,
试题分析:(1)连结OD,根据圆周角定理可得∠ADB=90°,即可求得∠ABD=60°,从而可以求得∠BDC=
 ,即可证得△ODB是等边三角形,则可得∠ODC=90°,问题得证;
,即可证得△ODB是等边三角形,则可得∠ODC=90°,问题得证;(2)根据平行线的性质可得∠OED=90°,根据垂径定理可得
 ,根据勾股定理可求得OE的长,然后根据∠DOC、∠DOF的正切函数即可求得CD、DF的长,从而可以求得结果.
,根据勾股定理可求得OE的长,然后根据∠DOC、∠DOF的正切函数即可求得CD、DF的长,从而可以求得结果.(1)连结OD

∵AB是⊙O的直径,
∴∠ADB=90°.
∵∠A=30°,
∴∠ABD=60°.
∵∠ABD=2∠BDC,
∴∠BDC=
 .
.∵OD=OB,
∴△ODB是等边三角形.
∴∠ODB=60°.
∴∠ODC=∠ODB+∠BDC=90°.
∴CD是⊙O的切线;
(2)∵OF∥AD,∠ADB=90°,
∴∠OED=90°
∵BD=OB=2,
∴
 .
.∴
 .
. ∵OD=OB=2,∠DOC=60°,∠DOF=30°,
∴
 ,
, .
.∴
 .
.点评:此类问题知识点较多,综合性较强,在中考中比较常见,一般难度不大,需熟练掌握.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
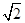 的弦所对的劣弧的弧长等于 。
的弦所对的劣弧的弧长等于 。 的距离为3,点P是直线
的距离为3,点P是直线


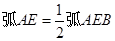 ,正确结论的个数是( )
,正确结论的个数是( )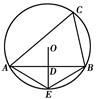

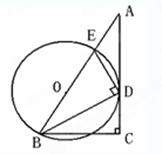
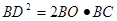 .
.

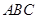 内接于
内接于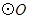 ,
,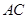 是
是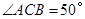 ,点D是弧BAC上一点,则
,点D是弧BAC上一点,则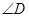 = °.
= °.
 的圆形纸片中剪下40%圆周的 一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为
的圆形纸片中剪下40%圆周的 一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为

