Question

【题目】如图某超市举行“翻牌”抽奖活动，在一张木板上共有6个相同的牌，其分别对应价值为2元、5元、8元、10元、20元和50元的奖品．
（1）小雷在该抽奖活动中随机翻一张牌，求抽中10元奖品的概率；
（2）如果随机翻两张牌，且第一次翻过的牌不再参加下次翻牌，求两次抽中的奖品的总价值大于14元的概率．

Answer 1

【答案】
（1）解：共有6个可能的结果，抽中10元奖品的结果有1个，

∴抽中10元奖品的概率为

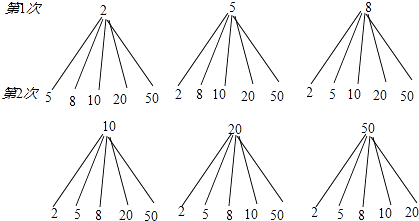
（2）解：画树状图：

共有30种可能的结果，两次抽中的奖品的总价值大于14元的结果有22个，

∴两次抽中的奖品的总价值大于14元的概率= = ．

【解析】（1）随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数，据此用1除以6，即可得出结果．（2）首先应用树状图法，列举出随机翻2张牌，所获奖品的总值一共有多少种情况；然后用两次抽中的奖品的总价值大于14元的情况的数量除以所有情况的数量即可．
【考点精析】关于本题考查的列表法与树状图法，需要了解当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率才能得出正确答案．