题目内容
【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长. 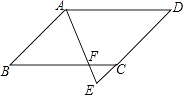
【答案】解:∵四边形ABCD为平行四边形, ∴AB=DC=3,AB∥DE,
∴△ABF∽△ECF,
∴ ![]() .
.
∵AB=3,EF=0.8,AF=2.4,
∴ ![]() ,
,
∴CE=1,
∴DE=DC+CE=3+1=4.
∵AB∥DE,
∴∠BAE=∠E.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠E=∠DAE.
∴AD=DE=4.
∴AD的长为4.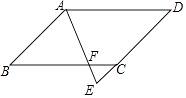
【解析】由平行四边形的性质得出AB∥CD,则△ABF∽△ECF,由该相似三角形的对应边成比例求得CE=1;得出内错角相等∠E=∠BAE,再由角平分线证出∠E=∠DAE,即可得出结论AD=DE=4.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】函数y=x2+3x+2的图象如图1所示,根据图象回答问题: 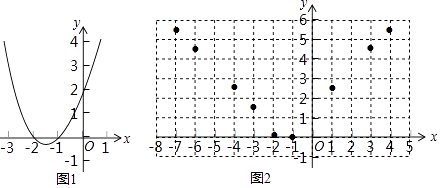
(1)当x时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题: ①函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
②如表是函数y= ![]() 的几组y与x的对应值.
的几组y与x的对应值.
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
③写出该函数的一条性质: .