��Ŀ����
����Ŀ���Ķ����ϣ�������⣮
����������ʽ![]() ��ֵ�dz���2����a��ȡֵ��Χ��2��a��4�� ��
��ֵ�dz���2����a��ȡֵ��Χ��2��a��4�� ��
������ԭʽ=|a��2|+|a��4|����|a|��ʾ��x�������ϵĵ㵽ԭ��ľ��룬|a��2|��ʾ��a�������ϵĵ㵽��2�ĵ�ľ��룬�������ǿ��Խ���������з�����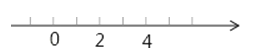
�⣺ԭʽ=|a��2|+|a��4|
�������Ͽ�������a����2��ʾ�ĵ���ߣ�����2��ʾ�ĵ����4��ʾ�ĵ�֮�仹������4��ʾ�ĵ��ұߣ������ɵ�a�ķ�ΧӦ��2��a��4��
��1��������Ľ�������������Щ��ѧ˼�룿���о٣�
��2������![]() ��
��
���𰸡��⣺��1�����ν��˼�룬��������˼�룮
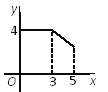
��2��ԭʽ=|3��a|+|a��7|
�ٵ�a��3ʱ��ԭʽ=3��a+7��a=10��2a��
�ڵ�3��a��7ʱ��ԭʽ=4��
�۵�a��7ʱ��ԭʽ=a��3+a��7=2a��10��
����������1���������еĽ�����̼��ɵó����ۣ�
��2����a��3��3��a��7��a��7��������������ۼ��ɣ�
�����㾫����������Ҫ�����˶��θ�ʽ�������뻯������֪ʶ�㣬��Ҫ����1��������������Ƿ���������С�������ʽ���������̵�����ƽ���������ʰ���д�ɷ�ʽ����ʽ��Ȼ�����÷�ĸ���������л���2�����������������������ʽ���Ƚ����Ƿֽ���������ʽ��Ȼ����ܿ��þ�������������ʽ������������ȷ�����⣮