题目内容
【题目】一个直角三角形的两条直角边分别长3cm,4cm,则它的内心和外心之间的距离为________
【答案】![]()
【解析】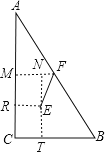
如图,E为直角三角形ABC的内心,F为直角三角形ABC的外心,
过E作ET⊥BC于T,ER⊥AC于R,过F作FM⊥AC于M,TE交FM于N,
则ER=ET,∠C=∠ERC=∠ETC=90°
∴ERCT是正方形,
∴ER=RC=CT=ET,
∵∠FMC=∠C=∠NTC=90°
∴四边形MCTN是矩形,
∴CT=MN,CM=NT,
∵F为AB中点,FM∥BC,
∴M为AC中点,
∴FM=![]() BC=1.5,MC=AM=2,
BC=1.5,MC=AM=2,
设直角三角形ABC的内切圆的半径是r,
则ER=RC=CT=ET,
根据切线长定理得:3r+4r=5,
r=1,
即ER=RC=CT=ET=MN=1,
∴MR=21=1,
在Rt△ENF中,EN=MR=1,FN=1.51=0.5,由勾股定理得:EF=![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目