题目内容
【题目】若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是( )
A.梯形
B.矩形
C.菱形
D.正方形
【答案】C
【解析】解:如图,AC=BD,E、F、G、H分别是线段AB、BC、CD、AD的中点, ∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,∴EH=FG= ![]() BD,EF=HG=
BD,EF=HG= ![]() AC,
AC,
∵AC=BD
∴EH=FG=FG=EF,
则四边形EFGH是菱形.故选C.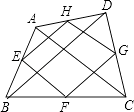
【考点精析】掌握三角形中位线定理和菱形的判定方法是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?