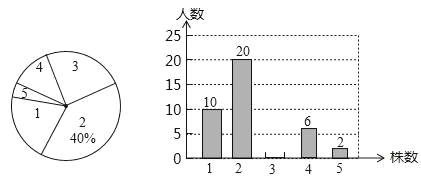
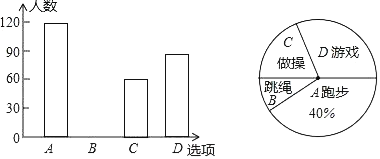
题目内容
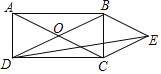
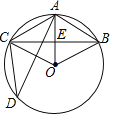
【题目】如图,在⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且sinD=![]() ,求证:四边形ABOC为菱形.
,求证:四边形ABOC为菱形.
【答案】证明见解析
【解析】
由垂径定理的推论求得∠AEB=90°,然后解直角三角形求得∠ABE=30°,然后由圆周角定理得到∠BAE=60°,从而判定△AOB是等边三角形,得到OA=AB=OB,然后由垂径定理求得AC=AB,从而根据四边相等的四边形是菱形即可判断.
解:∵点A是劣弧BC的中点,
∴OA⊥BC,
∴∠AEB=90°,
∵∠D=∠ABE,
∴sin∠D=sin∠ABE=![]() =
=![]() ,
,
∴∠ABE=30°,
∴∠BAE=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=OB,
∵OA⊥BC,
∴![]()
∴AC=AB,
∴AC=OC=OB=AB,
∴四边形ACOB是菱形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目