题目内容
【题目】在△ABC中，AB=AC=10，cosB= 
，如果圆O的半径为2 
，且经过点B、C，那么线段AO的长等于 ．
【答案】6或10
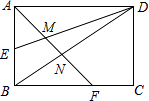
【解析】解：作AD⊥BC于D，如图， ∵AB=AC，
∴AD垂直平分BC，
∴点O在AD上，连接OB，如图，
在Rt△ABD中，cosB= 
= 
，
∴BD=10× =6，
∴AD= 
=8，
在Rt△BOD中，OD= 
=2，
∴OA=AD﹣OD=8﹣2=6．
或OA=AD+OD=8+2=10．
所以答案是6或10．
【考点精析】关于本题考查的等腰三角形的性质和垂径定理，需要了解等腰三角形的两个底角相等（简称：等边对等角）；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能得出正确答案．
练习册系列答案
相关题目
【题目】某校需要招聘一名教师，对三名应聘者进行了三项素质测试
下面是三名应聘者的综合测试成绩：
应聘者 成绩 项目 | A | B | C |
基本素质 | 70 | 65 | 75 |
专业知识 | 65 | 55 | 50 |
教学能力 | 80 | 85 | 85 |
（1）如果根据三项测试的平均成绩确定录用教师，那么谁将被录用？
（2）学校根据需要，对基本素质、专业知识、教学能力的要求不同，决定按2：1：3的比例确定其重要性，那么哪一位会被录用？
