题目内容
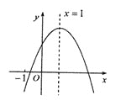
【题目】在平面直角坐标系 xOy 中,点A,B的坐标分别为(-2,0),(1,0).同时将点A ,B先向左平移1个单位长度,再向上平移2个单位长度,得到点A,B的对应点依次为C,D,连接CD,AC, BD .
(1)写出点C , D 的坐标;
(2)在 y 轴上是否存在点E,连接EA ,EB,使S△EAB=S四边形ABDC?若存在,求出点E的坐标;若不存在,说明理由;
(3)点 P 是线段 AC 上的一个动点,连接 BP , DP ,当点 P 在线段 AC 上移动时(不与 A , C 重合),直接写出CDP 、ABP 与BPD 之间的等量关系.

【答案】(1)C(﹣3,2),D(0,2);(2)存在,E(0,4)或(0,﹣4);(3)∠DPB=∠CDP+∠ABP
【解析】
(1)利用平移变换的性质解决问题即可.
(2)如图1中,设E(0,m),根据平行四边形和三角形的面积公式,构建方程即可解决问题.
(3)如图2中,作PH∥CD交BD于H.利用平行线的性质解决问题即可.
解:(1)如图1中,

∵点A,B的坐标分别为(﹣2,0),(1,0),将点A,B先向左平移1个单位长度,再向上平移2个单位长度,得到点A,B的对应点依次为C,D.
∴C(﹣3,2),D(0,2).
(2)如图1中,设E(0,m),
∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
∵S△EAB=S四边形ABDC,
∴3×2=![]() ×3×|m|,
×3×|m|,
∴m=±4,
∴E(0,4)或(0,﹣4).
(3)如图2中,作PH∥CD交BD于H.

∵AB∥CD,PH∥CD,
∴PH∥AB
∴∠CDP=∠DPH,∠ABP=∠BPH,
∴∠DPB=∠DPH+∠BPH=∠CDP+∠ABP.

【题目】为选派一名学生参加全市实践活动技能竞赛,A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)
平均数 | 方差 | 完全符合要求个数 | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
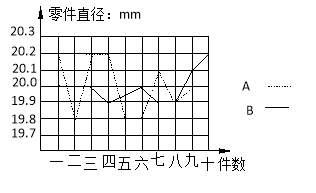
根据测试得到的有关数据,试解答下列问题:
⑴ 考虑平均数与完全符合要求的个数,你认为 的成绩好些;
⑵ 计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些;
⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由。
【题目】有20筐白菜,以每筐25千克为标准,超过或不足千克数分别用正,负数表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?