题目内容
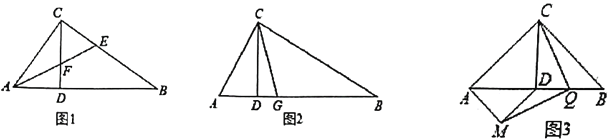
【题目】把正整数1,2,3,4……,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、…….用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A、B、C、D.设A=x.

(1)在图1中,2018排在第 行第 列;排在第m行第n列的数为 ,其中m≥1,1≤n≤8,且都是正整数;(直接写出答案)
(2)若A+2B+3D=357,求出C所表示的数;
(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.
【答案】(1)253,2;8m+n﹣8;(2)77;(3)这些数的和不能为4212,理由见解析.
【解析】
(1)每行8个数,2018=8×252+2,2018排在第253行第2列;第m行第8列数为8m,第m行第n列为8m+n﹣8;
(2)设A=x,可以依据A、B、C、D四个数排列的规律依次用含x的代数式表达,再根据题意列方程求解即可;
(3)根据题意列方程求出x,如果x为正整数,并且不在第6、7、8列,才能符合题目要求.
解:(1)∵2018=8×252+2,2018排在第253行第2列;根据数字排列规律:第m行最后一列数字为8m,∴排在第m行第n列的数为8m+n﹣8;
故答案为:253,2;8m+n﹣8;
(2)由题意得:A=x,B=x+24,C=x+27,D=x+3,
∵A+2B+3D=357,
∴x+2(x+24)+3(x+3)=357,
解得:x=50,
∴C=x+27=50+27=77.
(3)这些数的和不能为4212;
∵被阴影覆盖的这些数的和=x+1+x+2+x+8+x+9+x+10+x+11+x+16+x+17+x+18+x+19+x+25+x+26=12x+162
若12x+162=4212,则x=337.5不是正整数,不符合题意.
故答案为:(1)253,2;8m+n﹣8;(2)77;(3)这些数的和不能为4212,理由见解析.

【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.