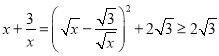题目内容
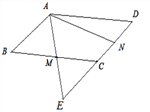
【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
【答案】![]()
【解析】分析:延长DC和AM交于E,过点E作EH⊥AN于点H,易证△ABM≌△ECM,再证得AB=![]() NE,因为AN=2,AE=2AM=2,且∠MAN=60°,可得∠AEH=30°,AH=
NE,因为AN=2,AE=2AM=2,且∠MAN=60°,可得∠AEH=30°,AH=![]() AE=1,根据勾股定理可得EH =
AE=1,根据勾股定理可得EH =![]() ,EN=2,即可得AB=
,EN=2,即可得AB=![]() .
.
详解:
如图,延长DC和AM交于E,过点E作EH⊥AN于点H.
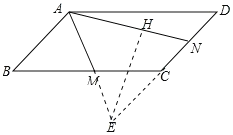
∵四边形ABCD为平行四边形,
∴AB∥CE,
∴∠BAM=∠CEM,∠B=∠ECM.
∵M为BC的中点,
∴BM=CM.
在△ABM和△ECM中,
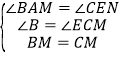 ,
,
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=![]() AB,即AB=
AB,即AB=![]() NE,
NE,
∵AN=2,AE=2AM=2,且∠MAN=60°,
∴∠AEH=30°,
∴AH=![]() AE=1,
AE=1,
∴EH=![]() =
=![]() ,
,
∴NH=AN-AH=2-1=1,
∴EN=![]() =2,
=2,
∴AB=![]() ×2=
×2=![]() ;
;
故答案为:![]() .
.

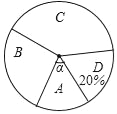
【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级 | A | B | C | D |
人数 | 6 | 10 | m | 8 |
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.