题目内容
【题目】首先，我们学习一道“最值”问题的解答：
问题：已知x＞0，求
的最小值．
解答：对于x＞0，我们有：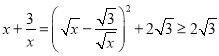
当
，即
时，上述不等式取等号，所以的最小值是
由解答知，的最小值是.
弄清上述问题及解答方法之后，解答下述问题：
（1）求
的最小值．
（2）在直角坐标系 xOy 中，一次函数
的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
①求 A 、 B 两点的坐标；
②求当OAB 的面积值等于
时，用b 表示 k ；
③在②的条件下，求AOB 面积的最小值.
【答案】（1）4；（2）①（-
，0）（0，b）；②k=
；③7+2
【解析】
（1）把原式化成平方的形式求解，即化成
=
求解即可.
（2）①一次函数
的图象与 x 轴、 y 轴分别交于 A 、 B 两点，分别令y=0 ，x=0，求出即可；
②用k和b表示出三角形的直角边的长，从而表示出面积，和△OAB的面积值等于|OA|+|OB|+3列成方程，用b表示k；
③设x=b-2，则b=x+2，根据题干中第二问所给的解答过程得到提示，配方后求得x成立时的最小值．
解：（1）=
∴
∴
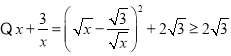
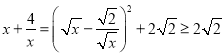
（2）①一次函数的图象与 x 轴、 y 轴分别交于 A 、 B 两点
∴分别令y=0 与x=0
∴当x=0时，y=b；当y=0时，x=-
∴A 、 B 两点的坐标分别为（-，0）（0，b）
②当x=0时，y=b；当y=0时，x=-．
所以|OA|=，|OB|=b．
∴S△OAB=
|OA||OB|=
．
∴=+b+3，
∴
=b+3，k=．
③S△OAB==
．
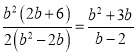设x=b-2，则b=x+2．
S△OAB=
=
=x+
+7
=(
)2+7+2≥7+2．
上述不等式等号在x=时成立．
故△OAB面积最小值是7+2．
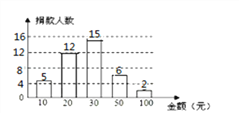
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查，并根据统计数据，制作了如图所示的统计表和统计图.
组别 | 视力 | 频数（人） |
|
| 20 |
|
|
|
|
|
|
|
| 70 |
|
| 10 |
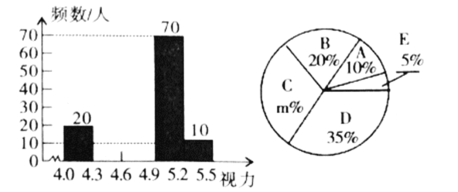
请根据图表信息回答下列问题：
（1）求抽样调查的人数；
（2）
___________，
_____________，
_____________；
（3）补全频数分布直方图；
（4）若视力在4.9以上（含4.9）均属正常，则视力正常的人数占被统计人数的百分比是多少？
